Homoclinicas e caos

Voltando ao assunto, conforme prometido há tempo, aqui vai, mais uma breve introdução tema.

No ano de 1686, a lei de Newton do movimento revolucionou a ciência:
F=Ma, a força (F) é igual à massa (M) vezes a aceleração (a).
Isto gera um sistema dinâmico governado por uma equação diferencial.




Seja x a distância a que uma nave espacial está da Terra, x’ a sua velocidade, taxa de variação de x, e x’’ a aceleração.
Então F=Mx’’ é a equação diferencial.
Esta é ainda a maneira ideal de modelar um sistema que evolui no tempo.
Dando as condições iniciais pode-se predizer com exactidão uma única solução.
Se, por exemplo, F=8000, e M=2, então x’’=4000.
Supondo que para t=0 conhecemos as condições iniciais x=700, x’=300, então a solução exacta é x=2000t2+300t+700. Ao fim de uma hora, quando t=1, a distância da terra é x=3000. E assim pode-se saber todo o percurso da nave com exactidão.

Em 1887 o rei da Suécia ofereceu um prémio a quem conseguisse responder à questão “Será o sistema solar estável?”
Poincaré, um matemático françês, ganhou o prémio, com o seu trabalho sobre o problema dos 3 corpos.
Ele considerou, por exemplo, apenas o Sol, a Terra e a Lua descrevendo órbitas planas sob acção das mútuas atracções gravitacionais.
Este sistema tem algumas soluções instáveis.



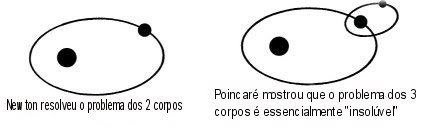
Introduzindo a chamada Secção de Poincaré, ele viu que podem ocorrer órbitas homoclínicas. Isto levaria ao caos e à impredictabilidade.

A rica dinâmica dum estado caótico permite frequentemente, controlá-lo.

É importante saber que os sistemas mais simples podem ter um comportamento muito complexo.
Isto deveria ser ensinado nas escolas.
Infelizmente os textos escolares limitam-se a tratar problemas solúveis, geralmente, lineares.
Porque levou 300 anos de Newton até à Teoria do Caos?
a) Porque não havia computadoes
b) Os investigadores procuravam a Ordem
c) Resultados aleatórios eram considerados errados, por isso acabavam no cesto dos papeis.

O pêndulo é um exemplo simples e clássico dum sistema dinâmico.
Durante um serviço religioso, Galileu observou a constante oscilação dum candeeiro, provocada por uma brisa suave.
O pêndulo tem sido usado, durante séculos, nos relógios e é um exemplo de regularidade e predictabilidade.
O seu movimento é descrito pela simples equação diferencial


O espaço de fase é o espaço das condições iniciais. Está cheio de trajectórias que não se cruzam.
Um movimento começado em qualquer ponto, tem um percurso único.
O espaço de fase dum pêndulo simples é a 2 dimensões.
Sistemas complexos têm centenas de dimensões.

Uma órbita homoclínica é geradora de caos.

Suponhamos um número muito pequeno, por exemplo, E (digamos 1/1000000000).
Larguemos o pêndulo em descanso, e quase no topo superior, mas exactamente a E graus do eixo vertical.
Durante anos ele lentamente aumentará de velocidade.
A certa altura fará uma rápida transição de 360º.
Depois durante anos abrandará até um ponto de repouso, a E graus do outro lado da vertical.
Se for perturbado, pode, ou não, rodar sobre o topo.
Mecanismo para o caos: uma perturbação regular, mais uma passagem repetida perto dum estado instável.




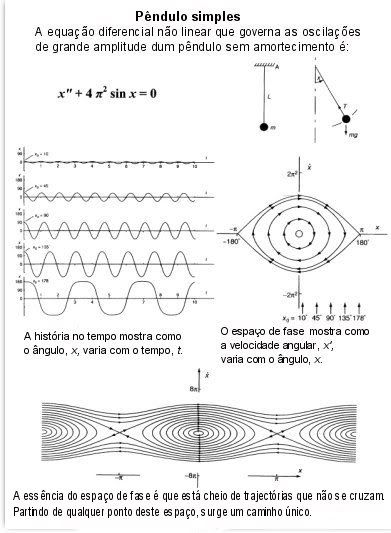
Mas o pêndulo que temos estado a descrever não é realístico. Ele oscila eternamente sem decréscimo da sua amplitude de deslocação.
O modelo matemático que usamos é incompleto. Ignorámos a fricção no ponto de apoio e a causada pelo ar na extremidade.
Ambas dissipam energia e abrandam o movimento do pêndulo.
Newton experimentou oscilar o pêndulo em vários fluidos e deduziu que o retardamento é proporcional à densidade do fluído. Para movimentos rápidos, o arrastamento D é proporcional ao quadrado da velocidade.




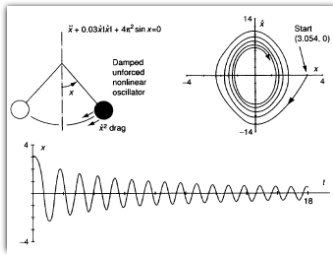
O amortecimento transforma órbitas fechadas em espirais que convergem para um ponto atractor.

Há 3 tipos de pêndulos:
• Um pêndulo simples, sem amortecimento, que oscila para sempre. Tem órbitas fechadas num espaço de fase a 2 dimensões.
• Um pêndulo simples, com amortecimento, que tende para um ponto de equilíbrio. Tem órbitas com a forma de espirais, num espaço de fase a 2 dimensões, que convergem para um ponto atractor.
• Um pêndulo forçado (driven), que tem um espaço de fase a 3 dimensões e pode exibir caos.




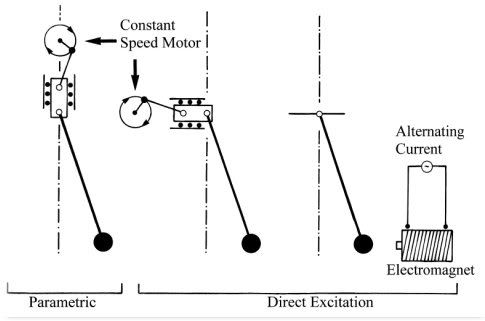
O pêndulo forçado tem um espaço de fase a 3 dimensões, o deslocamento (x), a velocidade (y=x’), e o tempo (t).




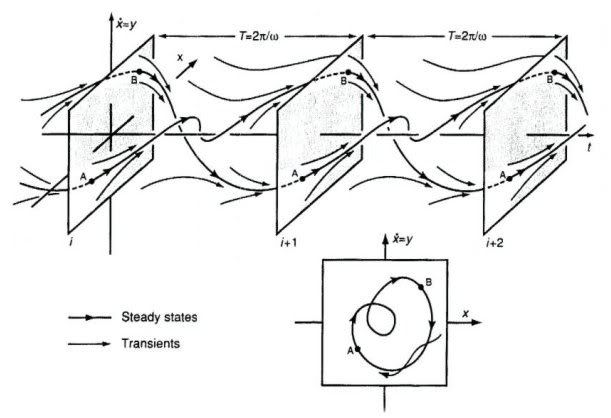
Um pêndulo forçado com amortecimento pode ser descrito pela equação diferencial : x’’+kx’+sen t =A cos wt.
Tomando uma secção estroboscópica, vê-se a lenta criação dum atractor estranho.

Se considerarmos 2 pêndulos idênticos, com posições iniciais ligeiramente diferentes, os seus movimentos tornam-se completamente diferentes e sem relação entre eles. Mas as suas secções estroboscópicas permanecem iguais.
(ver simulação)




Esta é uma possível definição de caos: uma extrema sensibilidade às condições iniciais.

(De: A Popular Pictorial Introduction to Chaos)